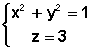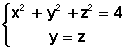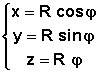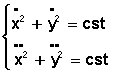- CINEMATIQUE du POINT -
Enoncés des Exercices
** Généralités # 1
Démontrez que la dérivée d'un vecteur, dont le module est constant, est toujours perpendiculaire à celui-ci.
** Généralités # 2
Dériver un vecteur unitaire par rapport à son angle polaire.
** Généralités # 3
1°) Déterminer l’expression de
l’aire du parallélogramme construit sur deux vecteurs 
2°) Déterminer l’expression du volume
du parallélépipède oblique construit sur trois vecteurs 
.
** Généralités # 4
Soit 2 vecteurs 
, on note 
leur somme et
leur
différence. Montrez:
1°) que si la somme et la différence ont le
même module, on déduit: 
2°) que si la somme et différence sont
perpendiculaires, on déduit : 
* Généralités # 5
Que représente, dans 
et puis dans 
, l'équation: 
?
* Généralités # 6
Que représente, dans et puis dans , l'équation: 
?
* Généralités # 7
Que représente, dans , les équations:
** Généralités # 8
Que représente, dans , les équations:
Retrouvez les expressions du vecteur
déplacement 
, conséquence de
l’accroissement séparé et indépendant de chacune des variables, puis celle du
vecteur position 
, dans le repère
local associé aux coordonnées polaires 
.
Retrouvez les expressions du vecteur
déplacement , conséquence de
l’accroissement séparé et indépendant de chacune des variables, puis celle du
vecteur position , dans le repère
local associé aux coordonnées cylindriques 
.
Retrouvez les expressions du vecteur
déplacement , conséquence de
l’accroissement séparé et indépendant de chacune des variables, puis celle du
vecteur position , dans le repère
local associé aux coordonnées cartésiennes 
.
Retrouvez les expressions du vecteur
déplacement , conséquence de
l’accroissement séparé et indépendant de chacune des variables, puis celle du
vecteur position , dans le repère
local associé aux coordonnées sphériques 
,
utilisées par les ingénieurs.
-
Retrouvez les expressions du vecteur
déplacement , conséquence de
l’accroissement séparé et indépendant de chacune des variables, puis celle du
vecteur position , dans le repère
local associé aux coordonnées sphériques, 
, utilisées par les navigateurs.
-
L’énergie cinétique d'un point
matériel a pour expression:
. Déterminer
son expression en coordonnées cartésiennes, polaires, cylindriques et sphériques.
** Vitesse # 2
Le mouvement d’un point M dans le plan est tel que:
où a et R sont des constantes positives.
1°) Déterminer la vitesse de ce point.
2°) Montrer que la vitesse est ici toujours perpendiculaire au vecteur position.
3°) Déterminer le module de la vitesse en fonction du temps.
4°)
Déterminer l'expression du vecteur unitaire tangent: 
en fonction du temps.
5°) Quelle est la distance parcouru s(t) à partir de t=0 ?
6°) Quelle est l’équation cartésienne de la trajectoire ?
** Vitesse # 3
Un "pistard" suit une trajectoire
dont l’expression en coordonnées polaires est: 
, avec une vitesse linéïque constante:
a et R sont des constantes positives.
1°) Déterminer l’expression de la trajectoire en coordonnées cartésiennes.
2°) Etablir l’expression de la vitesse dans la base polaire en fonction de j.
** Vitesse # 4
Une astéroïde suit la trajectoire en coordonnées polaires:
avec p = constante > 0. L’aire
balayée par 
est conservative:
Déterminer l’expression du moment de la vitesse en coordonnées polaires. Commenter le résultat.
** Vitesse # 5
Ayant aperçu un baigneur en difficulté sur
un lac, un sauveteur peut courir à la vitesse 
et nager à la vitesse 
.Pour effectuer le sauvetage dans le minimum de temps,
quelle est la relation que doivent vérifier les quantités: 
?
*** Vitesse # 6
Un électron dans un accélérateur suit la trajectoire polaire:
Etablir l’expression de la distance
parcourue lorsque: 
*** Vitesse # 7
Une bille roulant sur un plateau tournant suit
la trajectoire polaire:
, avec 
, où w et a sont des constantes positives. A l’instant initial: t=0 , j = 0.
1°) Déterminer l’expression de la vitesse en coordonnées polaires.
2°) Etablir l’expression de la distance parcourue, à l’instant t .
( On pourra utiliser la relation: 
)
*** Vitesse # 8
Un homme partant du point O décrit l'axe Oy' à la vitesse constante V ; son chien part du point A(a;0) et se dirige constamment vers son maître avec une vitesse dont le module constant vaut 2V.
1°) Quelle est la trajectoire du chien en coordonnées cartésiennes ?
2°) Combien de temps mettra le chien pour rattraper son maître ?
** Vitesse # 9
Quatre mouches Adèle, Berthe, Célestine et Dorothé sont initialement aux quatre sommets d'un carré de côté a . A vole vers B, B vole vers C, C vole vers D, D vole vers A, avec des vitesses de même module v .
Au bout de combien de temps les mouches se rejoignent elles ?
Un point se déplace sur un cercle suivant la loi, (dans le SI):
Si à la date t = 2 s, la
valeur de l'accélération totale est :
,
Quel est la valeur du rayon R du cercle?
** Accélération # 2
Un point répond à l'équation paramétrique :
1°) Quelle est l'équation de la trajectoire ?
2°) Que vaut le module de la vitesse en fonction du temps ?
3°) Exprimez les accélérations : tangentielle, normale et modulaire en fonction du temps.
La valve d'un vélo est à la distance R de
l'axe de la roue. Le cycliste procurant une vitesse constante 
à son vélo, donner l'expression du rayon
de courbure en fonction du temps : r = r(t) de la trajectoire suivie par la valve. (On admet, pour simplifier, que la
valve touche le sol).
** Accélération # 4
Un point M admet un mouvement tel que:
avec:
, w
et a
étant des constantes positives. A l'instant initial, M est confondu
avec l'origine.
1°) Rayon de courbure r = r(t) ?
2°) Equation cartésienne de la trajectoire ?
** Accélération # 5
On tire un projectile avec une vitesse de 600 m/s et suivant un angle de 60° avec l'horizontale. Avec: g = 9.81m.s-2, calculer:
1°) la portée horizontale
2°) la hauteur maximale atteinte
3°) la vitesse et la hauteur au bout de 30 secondes
4°) à quel moment et avec quelle vitesse, le projectile se trouve-t'il à 10 km de hauteur ?
** Accélération # 6
Avec: j = w t , w = cst, un point mobile décrit l'hélice d'équation :
Sachant que R=cst, donner en fonction de w et R l'expression de l'accélération normale aN .
** Accélération # 7
Un point se déplace en suivant un arc de cercle de rayon R. Sa vitesse dépend du chemin parcouru s selon la loi:
où k est une constante.
Déterminer l’expression de la tangente de l’angle a que fait le vecteur accélération résultante avec le vecteur vitesse en fonction de s .
** Accélération # 8
Un point est animé, dans un
plan, d’un mouvement tel que son accélération tangentielle soit:
,
et son accélération normale: 
,
où
a
et
b
sont des constantes positives. A
l’instant t = 0,
le point était au repos. Déterminer
en fonction du chemin parcouru s
le rayon de courbure r
de la trajectoire du point.
** Accélération # 9
Un point M décrit un cercle de rayon R et de centre O, de telle manière que l'angle au centre j varie avec le temps t selon la loi:
,
( j
en radians et
t en
secondes )
On désigne par a
l'angle que fait le vecteur accélération
avec le vecteur .
Donner l'expression de a
en fonction de t.
** Accélération # 10
En coordonnées polaires, sachant que a et w sont des constantes, le mouvement d’un point en fonction du temps est caractérisé par les relations:
Déterminer l’expression du rayon de courbure r de la trajectoire, en fonction du temps puis en coordonnées polaires.
*** Accélération # 11
Une courbe plane obéit à l'équation polaire:
p est une constante réelle positive, et e une constante réelle positive ou nulle. C étant une constante réelle positive, le mouvement d'un point sur cette courbe est tel que :
Déterminer et commenter l'expression du vecteur accélération en fonction de r
** Accélération # 12
Donner les caractéristiques du mouvement obéissant aux équations:
** Accélération # 13
Un projectile est lancé avec une vitesse initiale dont le module est
et faisant un angle a avec l'horizontale. En négligeant les frottements, déterminez l'expression du rayon de courbure initial de la trajectoire, en fonction de :
