Eléments de Solutions de l'Exercice

1°) Par définition la vitesse s'écrit :

ici:

en dérivant par rapport au temps t, il vient:

2°) Si c'est le cas, le produit scalaire de par sera nul. Calculons le:

3°) Le carré du module d'un vecteur, dans un repère orthonormé, est égal à la somme des carrés des composantes:

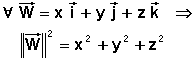
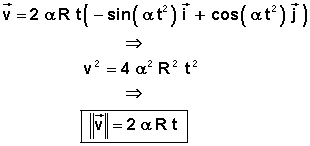
4°) Le vecteur unitaire tangent, est colinéaire et de même sens que la vitesse, il vient alors:

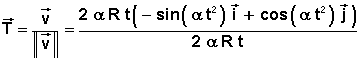
5°) La distance parcourue s s'obtient, par intégration, à partir du module de la vitesse:

la distance parcourue à l'instant initial, étant posée nulle il reste:

6°) Pour obtenir l'équation de la trajectoire, il faut l'extraire du mouvement caractérisé par le vecteur position:

Les composantes cartésiennes, ici s'expriment sous la forme:

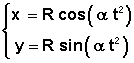
l'élimination du temps dans le système, s'effectue simplement:

il s'agit de l'équation d'un cercle, de rayon R , centré sur l'origine.