a la même longueur que la distance 
:Eléments de Solutions de l'Exercice
**Accélération # 3
Le mouvement de la valve est celui d'une cycloïde:
Le vélo roulant sans "glisser",
on déduit que l'arc
a la même longueur que la distance :
et la vitesse du vélo est liée à l'angle
par la
relation:
Le rayon de courbure sera déduit de l'équation:
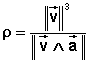
Il faut donc obtenir les expressions
de la vitesse et de l'accélération, que l'on déduira par dérivation du vecteur
position 
.
Ce dernier se décompose comme suit:
La base étant orthonormée, les vecteurs de bases vérifient les expressions:
Pour le module de la vitesse, calculons
le "carré" du vecteur 
,
c'est à dire son produit scalaire par lui même:
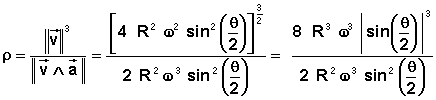
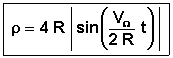
