Vecteur vitesse

Entre l'instant t et l'instant t + dt, le point M effectue un déplacement infinitésimal:

La direction de ce déplacement est tangentielle à la trajectoire. Nous désignerons par:

le vecteur unitaire tangent à la trajectoire à chaque instant. La valeur du déplacement effectué, durant le laps de temps infiniment petit, dt est aussi la distance parcourue sur la trajectoire:

Il est pratique, en distinguant la direction et le module, d'écrire le vecteur déplacement sous la forme:

figure: 6

Le rapport de ce déplacement sur le laps de temps est nommé vecteur vitesse, c’est la dérivée du vecteur position:

Il est commode d’écrire la vitesse sous la forme:

Attention la vitesse dépend du temps par son module et par sa direction :

Le vecteur tangent à une courbe, se détermine par la dérivation :

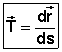
La vitesse s’obtenant en divisant le vecteur déplacement par le laps de temps, il vient immédiatement,

en coordonnées cartésiennes:

en coordonnées polaires:

en coordonnées cylindrique:

en coordonnées sphériques: