Courbure
En un point donné M d'une courbe (trajectoire), M', M" et M" définissent un seul cercle dans l'espace.
En passant à la limite correspondant à:
![]()
le cercle passant par M, M' et M" tend vers un cercle limite nommé cercle osculateur.
figure 7
Pour le point M, ce cercle est unique. Le rayon du cercle osculateur est encore nommé rayon de courbure. Son centre W est le centre de courbure de la courbe au point M.
On appelle osculateur le plan v contenant le cercle osculateur.
![]()
Dans plan osculateur v observons un déplacement infinitésimal:
figure 8
L'élément d'arc s'écrit: ![]() .
Le rayon de courbure est fonction du point considéré:
.
Le rayon de courbure est fonction du point considéré: ![]() .
La dérivée d'un vecteur unitaire par rapport à l'angle polaire est un vecteur
unitaire en quadrature avance:
.
La dérivée d'un vecteur unitaire par rapport à l'angle polaire est un vecteur
unitaire en quadrature avance:
![]()
![]()
Il vient:
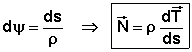
Pour une courbe plane, les vecteurs:
![]()
peuvent servir de base vectorielle locale autour de M:

La courbure est pour une trajectoire, la capacité de sa tangente à changer de direction. Plus précisément, nous définirons la courbure locale C, comme le module de la variation du vecteur tangent, par rapport au chemin parcouru ds:
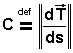
Figure: 9
![]()
La courbure est l'inverse du rayon de courbure, et de ce fait est toujours positive ou nulle:
![]()
![]()