Vecteur position

Le repère sert à définir la position du point. Le vecteur position est par définition le vecteur:

où O est l'origine du repère et M le point à repérer.

Avec un même repère, plusieurs systèmes de coordonnées peuvent être envisagés. Le choix des coordonnées sera gouverné par les symétries des problèmes traités. Dans la pratique les coordonnées orthogonales seront les seules utilisées. Parmi celles-ci les plus courantes sont: les coordonnées cartésiennes, polaires, cylindriques et sphériques. Donnons quelques éléments sur leur propriétés:

a) Coordonnées cartésiennes

Figure 2

Le vecteur position est par définition:

Pour définir le trièdre local associé aux coordonnées cartésiennes:

il faut construire le vecteur déplacement, consécutif aux accroissements séparés et indépendants des variable de position: x, y, z, c’est à dire:

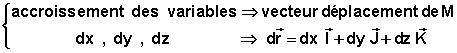
Pour les coordonnées cartésiennes,

reste uniforme.

Il est par ailleurs identique au trièdre du repère de référence. Il vient alors:

La position du point M, à chaque instant, sera exprimée à l’aide des coordonnées:

x = x(t) ; y = y(t) ; z= z(t)

ou bien avec la trajectoire et l’équation horaire:

f(x, y, z) = 0 ; g(x, y, z) = 0 et s = s(t)