Composition des accélérations

L'accélération du point M dans (O) sera par définition:

de même l'accélération de M dans (P):

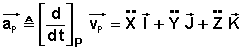
Figure 7

Décomposons le vecteur vitesse dans l'expression du vecteur accélération repéré dans (O):

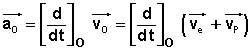
En reportant la vitesse d'entraînement:

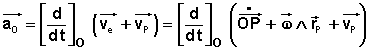
Le vecteur étant exprimé dans le repère (O), il est logique de poser:

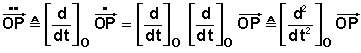
Pour les deux derniers termes, les vecteurs étant exprimés dans (P), développons l'opérateur:

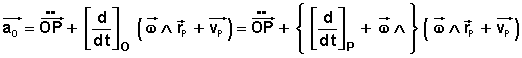
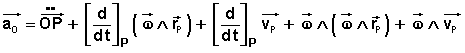
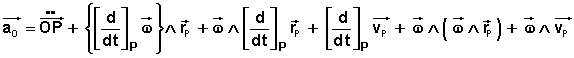
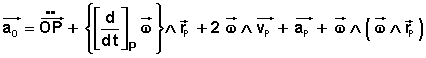
Pour traiter le terme où apparaît la dérivée de la vitesse angulaire, détaillons l'accélération angulaire exprimée dans le repère (O):

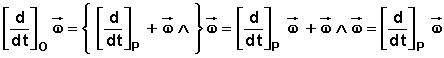
On notera alors sans ambiguïté l'accélération angulaire sous la forme:

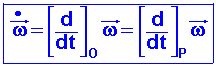
d'où:

Si le point M reste "attaché" au repère (P), c'est à dire que:

seule reste l'accélération d'entraînement:

Il est à noter que:

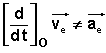
Cependant, si le point M se déplace à vitesse constante dans le repère (P), l'accélération dans ce repère reste nulle, mais il faut ajouter à l'accélération d'entraînement, un terme nommé accélération complémentaire où figure la vitesse par rapport à (P):

On qualifie encore l'accélération complémentaire comme: "accélération de Coriolis".

La composition des accélérations s'écrit alors: