Symétrie des repères

Le choix, consistant à désigner un repère comme fixe et l'autre comme mobile, est arbitraire. Pour deux repères en mouvement relatif, lors du traitement d'un problème, le choix du repère "fixe" peut se porter sur l'un ou sur l'autre.

Cependant il peut être intéressant dans certains cas, de changer de point de vue, et donc d'utiliser des formules de passage. Pour cela nous allons aménager les symboles et faire figurer en indices les repères avec lesquels on définit les composantes des vecteurs.

La vitesse angulaire du repère (P) évidemment exprimée dans le repère (O) sera dorénavant désignée par . De même on introduit la vitesse angulaire de (O) par rapport à (P) : .

Figure 8

De façon plus général on notera, par rapport au repère (O) "fixe":

et par rapport au repère (P) "fixe":

Le vecteur et ses dérivées seront toujours rapportés au repère "fixe" (O).

Le vecteur et ses dérivées seront toujours rapportés au repère "fixe" (P).

A l'aide de l'opérateur de dérivation, il est aisé de déduire les formules de passage suivantes:
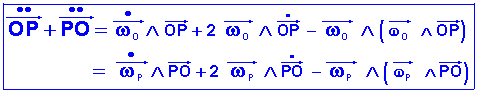