Dérivée d'un vecteur par rapport au temps

Pour un laps de temps déterminé dt, la variation d'un vecteur variable n'est pas évaluée de la même façon dans le repère "fixe" et dans le repère "mobile".

Figure 4

Considérons un vecteur variable , et exprimons le dans les deux repères:

sa dérivation par rapport au temps donne:

Détaillons ces expressions: on distingue en premier lieu la dérivée du vecteur lorsque le repère (O) est choisi comme "fixe":

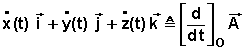
puis sa dérivée lorsque le repère (P) est choisi comme "fixe":

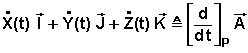
Et enfin un terme représentant la vitesse du vecteur "attaché" au repère "mobile" (P):

Ce qui donne la formule de dérivation (par rapport au temps) d'un vecteur exprimé dans les repères "fixe" et "mobile":

Cette expression est valide pour tout vecteur dépendant du temps.

Le repère "fixe" choisi étant (O), l'opérateur de dérivation par rapport au temps d'un vecteur, s'écrit:

Le repère "fixe" choisi étant (P), l'opérateur de dérivation par rapport au temps d'un vecteur, s'écrit: