Cinématique d'un "solide"

Dans le problème du changement de référentiels, il faut être capable de caractériser le mouvement d'un repère mobile par rapport à un certain repère "fixe" de référence. Cette exigence est identique à celle que l'on rencontre pour exprimer le comportement d'un solide en évolution. En fait en définissant un repère attaché au solide on obtient un repère mobile par rapport au repère de référence.

Figure 1

Notre repère de référence qualifié de "fixe" est ici (O):

(le symbole signifie par définition)

Le repère "mobile" est (P):

Dans le repère (O), le mouvement du repère mobile (P) est connu lorsque l'on donne la position du point P:

puis la position de l'axe de rotation D passant par P, caractérisé par le vecteur unitaire:

,

D'autre part, avec la convention habituelle de correspondance entre la rotation et la translation (règle du "tire-bouchon"), il est commode d'introduire le vecteur vitesse angulaire instantanée:

Le mouvement instantané du trièdre mobile (P) est donc complètement décrit par la connaissance simultanée des 2 vecteurs:

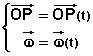
Les vecteurs de base du repère mobile sont variables:

cependant, ils restent orthonormés:

Durant le laps de temps dt, déterminons la variation infinitésimale du premier vecteur de base:

Figure 2

Pour cela de la figure 2 on déduit:

en posant:

comme:

et que d'autre part:

on synthétise ces résultats sous la forme:

En effectuant un calcul similaire pour les 2 autres vecteurs lors du même laps de temps infinitésimal dt, on obtient les relations fondamentales suivantes:

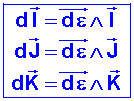
Notons, que pour des coordonnées orthogonales, si on connaît l'expression de , ces relations permettent la détermination aisée des différentielles multiples exprimées dans le repère local.

En les divisant par le laps de temps dt, il vient:

Ces équations permettent de caractériser le rotation instantanée d'un repère mobile ou d'un solide.