,
indéfiniment dérivables (infiniment lisses ), à
supports bornés, constitue l’espace vectoriel D.
Distributions
- Définition des distributions
- Distributions singulières
- Opérations élémentaires sur les distributions
- Dérivation au sens des distributions
- Convolutions
- Quelques propriétés de la famille "Dirac"
- Distributions tempérées
- Distributions causales
1. Espace vectoriel D
,
indéfiniment dérivables (infiniment lisses ), à
supports bornés, constitue l’espace vectoriel D.2. Distributions. Espace vectoriel D ’ = D *
On nomme fonctionnelle une application d’un espace fonctionnelle vers C .
On nomme distribution , toute fonctionnelle linéaire et continue sur D .
Soit
T
une distribution , on note 
, le scalaire correspondant à la fonction : 
.
Linéarité :
Si
converge vers
dans D
dans C
c’est à dire :
Les distributions formes un espace vectoriel
En particulier :
lorsque 
et 
(dual
topologique de D
) , 
est
une forme bilinéaire .
A toute fonction f(x) " localement sommable ", on peut associer une distribution f par la relation :
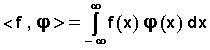
l’intégrale existe toujours puisque
( support borné ) , dans la suite on le notera sans les bornes :
f ou f(x) désigne indifféremment une fonction ou une distribution .
Si 2 distributions f et g vérifient la relation :
elles sont qualifiées de distributions identiques .
Deux fonctions localement sommables , "presque partout égales " (type CB) , définissent la même distribution .
_______
