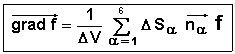Soit un champ scalaire ,

sa variation est donnée par:

Le gradient d’un champ scalaire f au point M est un vecteur dont:

1. la direction est celle de la variation la plus rapide du champ f
2. le sens correspond à la croissance du champ f
3. le module est la dérivée du champ par rapport au déplacement :

Les vecteurs du trièdre associé aux coordonnées orthogonales seront notés:

 

• coordonnées cartésiennes: f= f ( x , y , z )

pour celles-ci:

(somme sur les indices répétés)

• discrétisation cartésienne:

 

 

• coordonnées polaires:

 

 

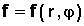
• coordonnées cylindriques:

 

 

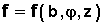
• coordonnées sphériques de l'ingénieur:

 

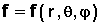
• coordonnées sphériques du navigateur:

 

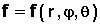
• autres coordonnées orthogonales:

 

 

.

.
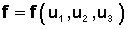