Cubique: équation algébrique du troisième degré
· Calcul numérique des racines
L’équation initiale :

sera souvent traitée sous sa forme simplifiée, en la divisant par a:

Le changement de variable :
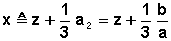
conduit à l’équation réduite :

où :

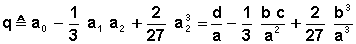
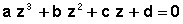
avec :
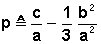

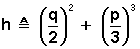
· Si h > 0 : 1 solution réelle et 2 complexes conjuguées :
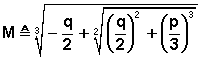
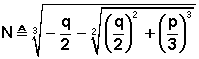
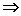
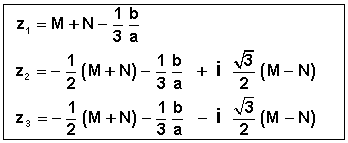
· Si h = 0, avec p = 0 et q = 0 : 1 solution réelle triple:
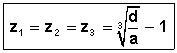
· Si h < 0 ou ( h = 0 avec p ¹ 0 et q ¹ 0 ) : 3 solutions réelles:


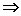
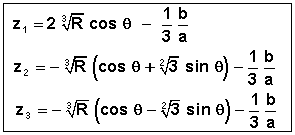
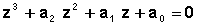
L’application directe des formules de Viète donne :
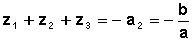
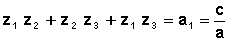
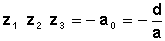
Leurs combinaisons permettent d’évaluer les sommes des puissances des racines:
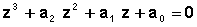
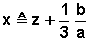
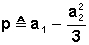


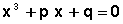
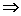
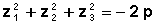
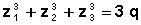


.
.